세그먼트 트리에 대한 글을 먼저 읽고 와 주시기 바랍니다.
앞서 주어진 배열 arr에 대해, 특정 구간의 합을 O(log N)의 시간 복잡도로 구할 수 있는 알고리즘인 segment tree에 대해 알아보았습니다.
주어진 배열 arr에 대해 미리 구간을 나누어 합을 구한 세그먼트 트리 tree를 만들고, 질의가 들어온 구간에 대해 대표 노드를 선별하여 그 값을 참조하는 방식입니다.
세그먼트 트리는 생성에 O(N log N), 구간 합 구하기에 O(log N), 특정 인덱스의 값 수정에 O(log N)의 시간 복잡도를 가집니다.
그렇다면 다음과 같은 경우를 생각해 봅시다.
"특정 구간의 값"을 변경하는 경우가 존재할 수 있습니다. 배열 arr에 대해 구간 [1, 3]의 값에 3씩 더하고, [2, 4]의 구간합을 구하는 식으로요.
이런 경우, 질의 한 번에 최악의 경우를 고려하면 O(N log )의 시간 복잡도를 가집니다. 이러한 질의가 k개 들어온다면, O(kN log N)의 시간복잡도를 가지게 되는 것이죠.
이러한 조건이 제시되는 문제 (링크)입니다. 이 문제의 경우 앞서 언급한 기본적인 세그먼트 트리를 사용해도 시간 초과가 납니다.
이런 문제를 어떻게 해결할 수 있을까요?
세그먼트 트리의 구조를 다시 생각해 봅시다.
루트 노드는 모든 구간을 포함하고, 자식 노드로 진행될수록 구간은 반씩 나뉘게 됩니다.
구간 합을 구하는 경우 해당 구간을 대표하는 노드를 찾아, 그 값을 참조합니다.
특정 인덱스의 값을 갱신하는 경우, 세그먼트 트리 내의 해당 인덱스를 포함하는 모든 노드의 값을 수정해야 합니다.
예를 들어 배열 arr = {1, 2, 9, 8, 4, 5, 3, 7} 이라고 합시다. 배열의 크기는 8입니다.
세그먼트 트리를 생성한다면 아래와 같은 형태가 됩니다.
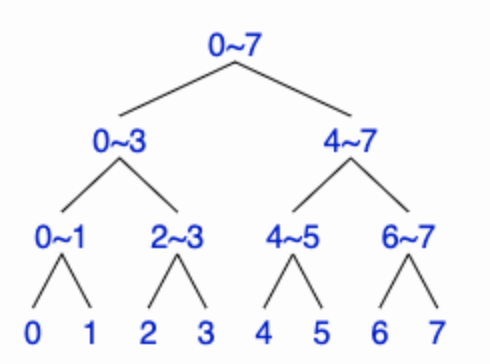

여기서 구간 [3, 5]의 값을 +2만큼 수정하고, 구간 [3, 7]의 합을 구한다고 가정해 봅시다.
기존의 세그먼트 트리라면 각 인덱스가 포함된 모든 노드의 값을 수정합니다. 인덱스 3에 대해 노드 2, 5, 11의 값을 수정하고, 인덱스 4에 대해 노드 3, 6, 12를 수정하며, 인덱스 5에 대해 노드 3, 6, 13을 수정합니다.
구간 [3, 7]의 합을 구할 때는 대표 노드인 11번 노드와 3번 노드의 합을 구하면 됩니다.
여기서 힌트를 얻을 수 있습니다.
우리는 3번, 11번 노드에만 접근하여 구간합을 구했지만, 우리가 미리 수정한 노드는 2, 3, 3, 5, 6, 6, 12, 13입니다.
즉 우리가 직접 접근하지 않을 노드에 대해 미리 수정을 해 두었다고 생각할 수 있습니다.
그렇다면 이 과정을 나중으로 미룬다면 시간복잡도를 많이 줄일 수 있지 않을까요?
이러한 아이디어를 느리게 갱신되는 세그먼트 트리 (lazy propagation in segment tree)라고 합니다.
직역하면 '게으르게 전파되는 세그먼트 트리'죠. 저는 느리다기보다는 게으르다는 표현이 더 어울리는 것 같습니다. 갱신을 뒤로 미루는 방식이니까요.
우리가 앞서 구간 [3, 5]에 대해 +2만큼 수정한다고 했었죠?
이를 느리게 수정되는 세그먼트 트리에서는 다음과 같이 정합니다.
위 구간을 대표하는 노드를 찾습니다. 예시의 경우 노드 11 (구간 3), 노드 6 (구간 4~5)이 대표 노드가 되겠습니다.
그리고, 해당 노드의 옆에 조그맣게 변화량을 적습니다. 이 수치를 lazy라고 하겠습니다.

세그먼트 트리를 그려 보았습니다. 대표 구간 노드에는 파란색으로 테두리를 그리고, 밑에 작은 동그라미를 달아 수정값을 표기하였습니다.
위 그림에서, 노드 6의 변화는 노드 12와 13에 전파되지 않았습니다. 즉, 값의 변화가 자식 노드에게 전파되는 것을 미룬 것입니다.
하지만 조상 노드의 경우, 수정된 값들을 적용해 주어야 합니다. 노드 1, 2, 3, 5의 값은 수정됩니다. 이는 재귀적으로 구현할 수 있습니다.
다음으로, 구간 [3, 7]의 합을 구하라는 질의가 들어옵니다. 대표 노드로는 노드 11 (구간 3)과 노드 3 (구간 4~7)이 선택됩니다.
노드 3의 경우, (저장된 값 8) + (lazy의 값 * 구간의 길이)로 값을 갱신하도록 합니다.
즉 8 + 2*1 = 10이 됩니다. 노드 11은 자식이 없으므로, lazy를 전파하지 않고 넘어갑니다.
노드 3의 경우, 앞서 노드 6을 수정하며 값이 함께 갱신되었으므로, 해당 값을 참조하면 됩니다.
이때 lazy가 남아있는 노드는 6번 노드 뿐입니다. 아직 노드 12, 13에 접근할 일이 없으므로 lazy는 전파되지 않은 채로 남아있게 됩니다.
그렇다면 구간 [2, 4]의 합을 구하는 경우에는 어떻게 될까요?
대표 노드로는 노드 5 (구간 2~3), 노드 12 (구간 4)가 선택됩니다.
노드 5는 앞서 이미 값이 갱신된 바 있으므로, 저장되어 있는 값 (19)를 꺼내어 오면 됩니다.
노드 12의 경우, 찾아 가는 과정은 1 -> 3 -> 6 -> 12가 됩니다. 이 중 노드 6에는 아직 lazy가 남아 있습니다.
따라서 노드 6의 값을 수정하고, lazy를 자식들 (노드 12, 13)에 전파하도록 합니다.
노드 6은 (저장된 값 9) + (lazy의 값 2 * 구간 길이 2) = 9 + 2 * 2 = 13이 됩니다.
따라서 노드 6의 값은 13이 되며, lazy는 자식 노드들에게로 전파됩니다.
다음으로 노드 12에 접근합니다. 노드 12는 lazy가 존재하므로, 위와 같은 과정을 반복하면 됩니다.
노드 12는 (저장된 값 4) + (lazy의 값 2 * 구간 길이 1) = 4 + 2 * 1 = 6이 됩니다.
따라서 구간 [2, 4]의 합은 19 + 6 = 25가 됩니다.
(그림 계속 그려 넣기가 너무 어려워서) 설명이 모호했는데...
코드와 함께 보시면 조금 이해가 쉬우실 겁니다.
우선 기존의 vector <long long> 형이었던 세그먼트 트리의 자료형을 수정해야 합니다.
pair <long long, long long>도 좋고, struct를 사용하여 더 직관적으로 자료형을 정의해도 좋습니다.
저는 자료형을 정의하여 사용해 보겠습니다.
typedef struct Tree {
long long value, lazy;
}Tree;
//n은 적당한 크기 (보통 배열의 길이 l * 4)
vector<Tree> tree(n);
long long segment_tree (int start, int end, int node) {
if (start == end) return tree[node].value = numbers[start];
int mid = (start + end) / 2;
return tree[node].value = segment_tree(tree, start, mid, node*2) + segment_tree(tree, mid+1, end, node*2 + 1);
}
arr를 이용하여 세그먼트 트리를 생성하는 과정은 똑같습니다. 다른 점은 tree의 각 노드에 구간합 값 value와 lazy값 lazy가 별개로 존재한다는 점입니다.
lazy는 모두 맨 처음에는 0으로 초기화되어 있습니다.
tree의 주어진 구간을 수정하는 함수는 다음과 같습니다.
void update_range (int start, int end, int node, int left, int right, long long value) {
//lazy가 남아있는 경우
if (tree[node].lazy != 0) {
tree[node].value += (end-start+1) * tree[node].lazy;
if (start != end) {
tree[node*2].lazy += tree[node].lazy;
tree[node*2+1].lazy += tree[node].lazy;
}
tree[node].lazy = 0;
}
if (right < start || left > end) return;
//대표 구간을 찾았을 때
if (left <= start && right >= end) {
tree[node].value += (end-start+1) * value;
if (start != end) {
tree[node*2].lazy += value;
tree[node*2+1].lazy += value;
}
return;
}
int mid = (start + end) / 2;
update_range(start, mid, node*2, left, right, value);
update_range(mid+1, end, node*2+1, left, right, value);
//부모 노드를 재귀적으로 갱신함
tree[node].value = tree[node*2].value + tree[node*2+1].value;
}
코드가 조금 긴데, 천천히 읽어 보면 이해할 수 있습니다. 기존 세그먼트 트리 코드와 비교해 보면 더 좋습니다.
앞서 lazy가 남아있는 경우, 해당 노드의 값을 갱신합니다. (기존값 + lazy * 구간의 길이)
또한 자식 노드가 존재하는 경우, lazy를 두 자식 노드에게 전파합니다.
이후 해당 노드의 lazy는 역할을 다했으므로 값을 0으로 바꾸어 줍니다.
다음으로, 구간을 대표하는 노드를 찾은 경우에 대한 코드입니다.
마찬가지로 노드의 값에 (value * 구간의 길이)의 값을 더해 줍니다. value는 구간에 대해 수정하는 값입니다.
이는 자식 노드들에게는 lazy가 되므로, 자식 노드들의 lazy 항목에 value를 기록하고, 함수를 종료합니다.
대표 구간이 아닌 경우, 재귀적으로 구간을 나누어 구간을 수정하는 함수를 호출하게 됩니다.
호출한 후, 자식 노드에서 값의 변경이 이루어진 것을 부모 노드에도 반영해야 하므로, 부모 노드의 value 값을 두 자식 노드의 value의 합으로 갱신해 줍니다.
마지막으로 tree의 구간합을 구하는 함수는 다음과 같습니다.
long long get_sum (int start, int end, int left, int right, int node) {
//lazy가 남아있는 경우
if (tree[node].lazy != 0) {
tree[node].value += (end-start+1) * tree[node].lazy;
if (start != end) {
tree[node*2].lazy += tree[node].lazy;
tree[node*2+1].lazy += tree[node].lazy;
}
tree[node].lazy = 0;
}
if (left > end || right < start) return 0;
if (left <= start && end <= right) return tree[node].value;
int mid = (start + end) / 2;
return get_sum(start, mid, left, right, node*2) + get_sum(mid+1, end, left, right, node*2 + 1);
}
여기도 마찬가지로 기존과 큰 차이는 없지만, lazy가 존재하는 경우에 대한 처리를 추가하였습니다.
lazy가 남아있는 경우, 이를 계산하여 기존 값에 반영하고, 자식 노드가 존재하는 경우 자식 노드들에게 lazy를 전파합니다.
이후 대표 구간 노드를 찾은 경우 해당 노드의 값을 return 하고, 그렇지 않은 경우 구간을 반으로 나누어 재귀적으로 구간합 함수를 호출합니다.
맨 처음에 언급할 때 특정 구간의 값을 업데이트 하는 경우 O(N log N)의 시간 복잡도를 가진다고 했었죠?
느리게 갱신되는 세그먼트 트리를 이용하면 O(log N)의 시간 복잡도 이내에 구간의 값을 수정할 수 있습니다.
느리게 갱신되는 세그먼트 트리를 이용하는 문제는 여기를 참고해 주세요.
내용 참고:
트리를 그릴 때 아이패드 같은 게 있으면 더 깔끔하게 그려서 업로드할 수 있을 텐데 아쉽네요 ㅠ
'알고리즘, 문제해결 > 알고리즘, 자료구조' 카테고리의 다른 글
| [Java] Java에서 사용하는 여러 자료구조 정리 (0) | 2021.10.18 |
|---|---|
| 세그먼트 트리 (0) | 2021.09.25 |
| C++의 auto에 대해 (0) | 2021.08.31 |
| [SQL] String, Date (0) | 2021.03.11 |
| [SQL] JOIN (0) | 2021.03.11 |


댓글