그리디 (Greedy Method) 알고리즘에 대해 다루어보고자 합니다.
Greedy는 한국어로 번역하여 탐욕법, 또는 욕심쟁이 알고리즘이라고도 합니다.
그리디 알고리즘이라고도 하는데, 개인적으로 알고리즘보다는 방법 (method)이 더 어울리는 표현이라고 생각합니다.
이하 '그리디 알고리즘' 이라고 표현을 통일하겠습니다.
그리디 알고리즘은 이름에서 알 수 있듯, 단순하게 탐욕적으로 문제를 해결하는 방법을 의미합니다.
즉, 지금 당장 현재 상황에 가장 좋은 선택지를 고르는 방법을 뜻합니다.
중요한 점은 이 선택이 추후에 미칠 영향에 대해서는 고려하지 않는다는 점입니다. 따라서 최적해를 보장하지는 않습니다.
그리디 알고리즘은 그 의미가 매우 넓습니다.
두루뭉실하게 '현재 가장 좋은 선택지를 고른다'고 뜻이 정의되어 있기에, 많은 알그리즘이 그리디 알고리즘으로 분류되기도 합니다.
그만큼 모든 경우를 전부 암기하거나 익혀둘 수는 없지만, 반대로 미리 특정 알고리즘을 암기해두지 않아도 되기도 합니다.
저도 실제로 코딩 테스트 문제를 풀던 중, 수학적 구현으로 접근해도 풀기 어려웠던 문제를 그리디 알고리즘을 이용하여 쉽게 풀었던 적이 있습니다. 제가 연습이 더 많이 되어 있었다면, 그 문제는 그리디로 푸는 것이 가장 쉽고 효율적이라는 것을 더 빨리 알아챘겠다는 아쉬움이 있었습니다.
보통 이러한 그리디 알고리즘을 이용하여 푸는 문제들은, 기준에 따라 좋은 것을 선택하는 문제들입니다.
따라서 문제에서 '가장 큰 순서대로', '가장 작은 순서대로' 등등 나름의 기준을 제시해 줍니다.
또, 정렬 알고리즘과 결합하여 문제가 출시되는 경우도 많습니다.
그리디 알고리즘의 가장 대표적인 예는 거스름돈 문제입니다.
다음 문제를 예로 들어 보겠습니다: www.acmicpc.net/problem/5585
5585번: 거스름돈
타로는 자주 JOI잡화점에서 물건을 산다. JOI잡화점에는 잔돈으로 500엔, 100엔, 50엔, 10엔, 5엔, 1엔이 충분히 있고, 언제나 거스름돈 개수가 가장 적게 잔돈을 준다. 타로가 JOI잡화점에서 물건을 사
www.acmicpc.net
동전은 500, 100, 50, 10, 5, 1엔 총 6종류가 있습니다. 사려는 물건의 가격은 1엔 이상 1000엔 미만입니다.
물건을 사려고 1000엔 지폐를 건냈을 때, 받게 되는 거스름돈 동전의 최소 갯수를 구하는 문제입니다.
이 문제를 어떻게 풀지에 앞서 그리디 알고리즘을 다시 한 번 상기해 봅시다.
그리디 알고리즘은 '당장 가장 좋은 최적의 선택지를 고르며, 이 선택지가 이후에 미칠 영향에 대해서는 고려하지 않는' 알고리즘입니다.
그렇다면 거스름돈 동전의 갯수가 최소가 되려면 어떻게 해야 할까요?
사려는 물건의 가격이 380엔이라고 가정합시다. 거스름돈은 1000 - 380 = 620이 됩니다.
620엔을 동전들의 조합으로 만드는 경우의 수는 여러 가지가 있을 것입니다. 1엔짜리 620개, 1엔짜리 5개와 5엔짜리 123개, 100엔짜리 6개와 10엔짜리 20개, 500엔짜리 1개와 100엔짜리 1개, 10엔짜리 2개...
이 규칙을 조심스럽게 관찰해 보면, 중요한 규칙을 찾을 수 있습니다.
큰 액수의 동전을 우선하여 고르면 전체 동전의 갯수는 최소가 됩니다.
500엔은 100엔짜리 5개로도 만들 수 있지만, 500엔짜리 동전 1개만으로도 만들 수 있습니다.
즉, 가장 큰 단위의 동전부터 돈을 거슬러 주면 됩니다.
그리디 알고리즘의 방법과 일치함을 확인할 수 있습니다.
당장 거슬러 줄 수 있는 가장 큰 단위의 동전부터 확인을 하는 겁니다.
620엔을 거슬러 주는 경우를 예로 들어 봅시다.
동전의 단위는 큰 순서대로 정렬하면 500, 100, 50, 10, 5, 1 입니다.
620은 500보다 크므로, 500엔 동전을 1개 거슬러 줄 수 있습니다. 이때 남은 거슬러 줄 비용은 220엔입니다.
220은 500보다 작으므로, 500엔 동전은 더 이상 거슬러 줄 수 없습니다. 다음 순서인 100보다는 크므로, 100엔 동전을 2개 거슬러 줄 수 있습니다. 이때 남은 거슬러 줄 비용은 20엔입니다.
20은 100보다 작고, 50보다 작습니다. 따라서 100엔, 50엔 동전은 더 이상 거슬러 줄 수 없습니다. 다음 순서인 10보다는 크므로, 10엔 동전을 2개 거슬러 줄 수 있습니다. 이때 남은 거슬러 줄 비용은 0엔입니다.
따라서 500엔 1개, 100엔 1개, 10엔 2개, 총 4개의 동전으로 620엔을 거슬러 줄 수 있으며, 이는 가능한 경우의 수 중 최소 갯수입니다.
위 과정을 그대로 코드로 옮겨 보겠습니다.
동전의 종류의 수가 K개라고 하면, 위 알고리즘의 시간복잡도는 O(K)가 됩니다. 동전의 종류에만 영향을 받고, 거슬러줘야 하는 금액의 크기와는 무관함을 확인할 수 있습니다.
그리디 알고리즘은 모든 문제에 적용할 수 있는 것은 아닙니다. 가장 중요한 것은 '그리디 알고리즘이 답을 보장해줄 수 있는가?' 입니다.
아래와 같은 경우를 봅시다.
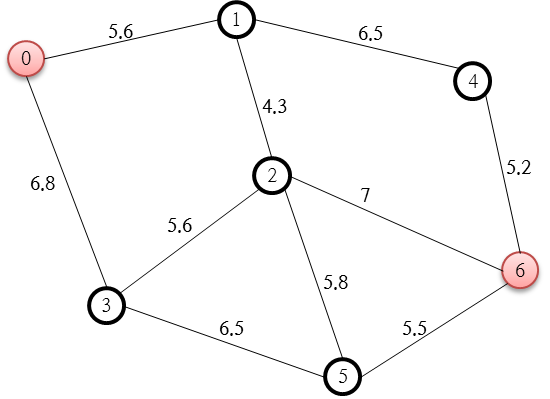
0에서 출발해서 5번까지 간다고 해 봅시다. 그리디 알고리즘을 사용한다면, 당장 거리가 짧은 노드를 향해 이동하게 되고, 나중에 미칠 결과에 대해서는 고려하지 않습니다.
위 과정대로 이동한다면 0 > 1 > 2 > 3 > 5 의 순서로, 총 22의 cost를 가지게 됩니다.
하지만 0 > 3 > 5 의 순서대로 이동한다면 13.3의 cost로 5에 도착할 수 있죠. 즉 위 문제에서는 그리디 알고리즘이 그다지 효과적이지 않은 겁니다.
앞에서 다룬 거스름돈 문제에서는, '가치가 큰 동전부터 우선해서 낸다면 최적의 해가 나온다' 는 보장이 있었기 때문에 그리디 알고리즘을 사용할 수 있었습니다. 더 구체적으로는, 각 동전의 단위가 큰 동전이 작은 동전의 배수의 형태를 취하므로 가능했습니다. 만약에 800원을 지불해야 하는데, 500, 400, 300, 200, 100원짜리 동전이 있다면 그리디 알고리즘은 500 + 100 + 100 + 100 = 4개라는 결과를 내놓겠지만, 사실 400원짜리 동전 2개만으로도 800원을 거슬러 줄 수 있습니다.
따라서, 그리디 알고리즘으로 문제를 해결할 때는 늘 그 해결법이 정당한지 검토해야 합니다. (매우 중요)
제가 풀어봤던 그리디 알고리즘 문제들을 몇 개 나열하는 것으로 글을 마치겠습니다.
브론즈 1 - 설탕 배달: www.acmicpc.net/problem/2839
실버 3 - ATM: www.acmicpc.net/problem/11399
골드 4 - 단어 수학: www.acmicpc.net/problem/1339
골드 2 - 보석 도둑: www.acmicpc.net/problem/1202
*본 글은 "나동빈, 이것이 취업을 위한 코딩 테스트다 with 파이썬" (한빛미디어, 2020)" 를 참고하여 작성하였습니다.
'알고리즘, 문제해결 > 알고리즘, 자료구조' 카테고리의 다른 글
| DFS/BFS (0) | 2021.02.02 |
|---|---|
| 구현 (0) | 2021.02.01 |
| Longest Common Subsequence/Substring (LCS) Algorithm (0) | 2020.11.15 |
| 비트마스크 (Bitmask) 연산 (0) | 2020.05.29 |
| 문자열 인코딩 (Run Length Encoding; RLE Algorithm) (0) | 2020.05.06 |

댓글